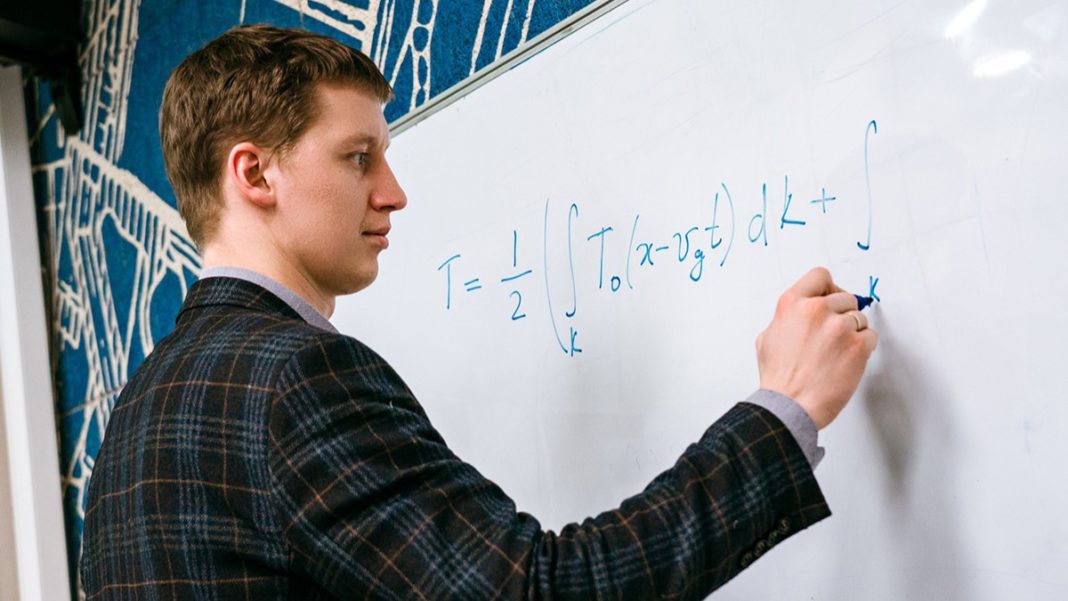NEW MEXICO: In the realm of scientific mysteries, few have captured the imagination of physicists quite like the Fermi-Pasta-Ulam-Tsingou (FPUT) paradox.
In the 1950s, this paradox originated from an unexpected discovery, challenging our understanding of nonlinear dynamics. It has recently unveiled groundbreaking insights that could reshape our perception of the universe.
The story begins in 1953, when physicists Enrico Fermi, John Pasta, Stanislaw Ulam, and Mary Tsingou set out to explore the behaviour of vibrating chains of particles.
Armed with state-of-the-art computers at the Los Alamos National Laboratory, they aimed to simulate the energy transfer in these systems, expecting that the energy would gradually disperse among the particles and reach a state of equilibrium.
To their astonishment, the team discovered something entirely unexpected. Despite their initial assumptions, the energy did not dissipate as predicted.
Instead, it exhibited a peculiar behaviour known as “recurrence,” repeatedly returning to its initial state before continuing to evolve. This persistent recurrence, which contradicted their expectations, is called the Fermi-Pasta-Ulam-Tsingou paradox.
The paradox sparked a flurry of scientific inquiries and prompted researchers to investigate the underlying mechanisms. As scientists delved deeper, they realized that the Fermi-Pasta-Ulam-Tsingou paradox was a manifestation of the intricate dance between nonlinearity and integrability.
The Fermi-Pasta-Ulam-Tsingou paradox revealed that nonlinear systems involving more complex interactions held untapped secrets that could revolutionize our understanding of dynamics.
Over the following decades, mathematicians and physicists from diverse fields engaged in a quest to unravel the enigma.
They explored various methods, from numerical simulations to analytical techniques, to comprehend the mechanisms governing the recurrence observed in the FPUT paradox.
Recent breakthroughs have shed new light on this long-standing puzzle. Researchers discovered that the recurrence of the FPUT paradox arises from a phenomenon known as soliton formation. Solitons are localized waves that maintain their shape and speed even when interacting with other particles.
These robust structures, acting as energy carriers, prevent complete energy dispersion in the system, leading to the recurrent behaviour observed in the paradox.
Moreover, the Fermi-Pasta-Ulam-Tsingou paradox has transcended its original context and found connections in various fields of science.
The paradox has inspired new research in nonlinear dynamics, statistical mechanics, and even quantum mechanics, pushing the boundaries of knowledge in these disciplines.
The implications of this paradox extend far beyond theoretical physics. Understanding the intricate dynamics of nonlinear systems has practical applications in fields such as engineering, materials science, and climate modelling.
By unravelling the secrets of the FPUT paradox, scientists can gain insights into the behaviour of complex systems, leading to advancements in technology, design, and our understanding of the natural world.
As scientists continue to delve into the Fermi-Pasta-Ulam-Tsingou paradox, they are opening doors to a new frontier of knowledge.
By challenging our assumptions and expanding our understanding of nonlinear dynamics, this paradox beckons us to explore the hidden intricacies of the universe, offering the promise of breakthroughs that may reshape our perception of reality.
Also Read: Unravelling the Freezing Paradox: Scientists Shed Light on a Mind-Boggling Phenomenon